Рекурсия (PascalABC.NET)

Вспомните, что факториал натурального числа n вычисляется как произведение всех натуральных чисел от 1 до n включительно. Факториал единицы равен единице и записывается это так: 1! = 1. Мы можем найти факториал, используя рекуррентную формулу

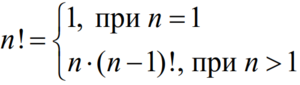
Рекурсивная функция обращается сама к себе. Но поскольку это не может продолжаться бесконечно, требуется определить условие выхода из процесса рекурсии. В нашем случае это равенство единице аргумента. Посмотрим, как вычисляется 5!

5! = 5∙4! = 5∙4∙3! = 5∙4∙3∙2! = 5∙4∙3∙2∙1! = 5∙4∙3∙2∙1 = 120

Если мы напишем рекурсивную функцию Fact(n), то при вызове Fact(5) она обратится сама к себе 4 раза. Количество таких обращений называется глубиной рекурсии. Если глубина рекурсии большая, ресурсов компьютера может не хватить, что необходимо учитывать при написании рекурсивных функций. Рекурсия может быть сведена к итерации, но к сожалению, этот процесс не всегда прост.

1 function Fact(n: integer): real := n = 1 ? 1.0 : n * Fact(n - 1);
2 
3 begin
4   Print(Fact(5));
5 end.

120

Возможна и иная запись функции

1 function Fact(n: integer): real := if n = 1 then 1.0 else n * Fact(n - 1);

Для нужд, в частности, комбинаторики факториал дополняется возможностью принимать аргумент, равный нулю. Принято считать по определению, что 0! = 1.

1 function Fact(n: integer): real := if n <= 1 then 1.0 else n * Fact(n - 1);

Программирование рекурсивных функций отличается простотой, а код – наглядностью. Плата за это – расход ресурсов компьютера. Рекурсия может быть достаточно сложной, например, параметры рекурсивной функции могут иметь, в свою очередь, рекурсивное определение. Типичный представитель – функция Аккермана A(n, m). Она растёт очень быстро, например, число A(4, 4) уже настолько велико, что количество цифр в нем во много раз превосходит количество атомов в наблюдаемой части вселенной. А вот значение A(3,4) можно попробовать вычислить.