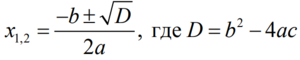Алгоритмы без множественного выбора (PascalABC.NET): различия между версиями
(Новая страница: «{{TOCRight}} == Поиск минимумов и максимумов == Найти минимальное из двух произвольных чисел. Е...») |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 37: | Строка 37: | ||
Print('Максимум:', Max(a, b, c)); | Print('Максимум:', Max(a, b, c)); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | == Процент отклонения значения максимального из чисел от среднего значения == | ||
Даны четыре натуральных числа. Найти процент отклонения значения максимального из чисел от среднего значения всех чисел с точностью до двух знаков после запятой. | Даны четыре натуральных числа. Найти процент отклонения значения максимального из чисел от среднего значения всех чисел с точностью до двух знаков после запятой. | ||
| Строка 51: | Строка 53: | ||
Введите четыре целых числа: 29 31 32 31 | Введите четыре целых числа: 29 31 32 31 | ||
Отклонение составляет 4.07% | Отклонение составляет 4.07% | ||
| + | |||
| + | == Анализ цифр в числе заданной разрядности == | ||
| + | Если заданное трехзначное число читается одинаково слева направо и справа налево, вывести «Да». В противном случае вывести «Нет». | ||
| + | Число трехзначное, поэтому для выполнения приведенного в задании условия достаточно, чтобы первая цифра числа равнялась последней. | ||
| + | <syntaxhighlight lang="pascal" line> | ||
| + | ## | ||
| + | var n := Abs(ReadInteger('Введите трехзначное число:')); | ||
| + | Print(if n div 100 = n mod 10 then 'Да' else 'Нет'); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Введите трехзначное число: 161 | ||
| + | Да | ||
| + | |||
| + | == Решение линейных и квадратных уравнений == | ||
| + | === Линейное уравнение === | ||
| + | Линейное уравнение имеет вид ax + b = 0, где a ≠ 0. Его решением (корнем) является значение x = -b / a. В некоторых задачах, особенно олимпиадных, намеренно содержащих препятствия к получению корректного решения, значение a = 0 также считается допустимым, несмотря на то, что математически оно приводит к вырожденности линейного уравнения – об этом следует помнить. | ||
| + | |||
| + | Вычисление х производится при помощи операции деления «/», перед делением операнды приводятся к вещественному типу, так что лучше сразу определить для переменных a и b тип real. | ||
| + | |||
| + | Написать программу для решения уравнения ax + b = 0. Значения a и b ввести с клавиатуры. Рассмотреть случаи, когда уравнение может иметь множество корней или не иметь корней вообще. | ||
| + | |||
| + | Корень линейного уравнения определяется по формуле x = -b / a. При a = 0 возможны два случая. Если b = 0, исходное уравнение обращается в тождество 0 ≡ 0 при любом х и корней бесчисленное множество. При b ≠ 0 исходное уравнение принимает вид b = 0, что противоречит рассматриваемому значению, поэтому уравнение в этом случае корней не имеет. Для коэффициентов а и b выбираем тип real. Следует помнить, что если взять значение а достаточно близким к нулю, появится шанс получить «машинную бесконечность». | ||
| + | |||
| + | <syntaxhighlight lang="pascal" line> | ||
| + | ## | ||
| + | var (a, b) := ReadReal2('Введите коэффициенты a и b:'); | ||
| + | if a = 0 then | ||
| + | if b = 0 then | ||
| + | Print('Корней бесконечное множество') | ||
| + | else | ||
| + | Print('Корней нет') | ||
| + | else | ||
| + | Print('x =', -b / a); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Введите коэффициенты a и b: 0.18 3.173 | ||
| + | x = -17.6277777777778 | ||
| + | |||
| + | === Квадратное уравнение === | ||
| + | Квадратное уравнение в общем виде записывается как | ||
| + | ax<sup>2</sup> + bx + c = 0, где a ≠ 0. Такие уравнение обычно решают при помощи вычисления вспомогательной величины – дискриминанта. Дискриминант определяется формулой D = b<sup>2</sup> – 4ac. | ||
| + | * Если дискриминант положительный, уравнение имеет два разных действительных корня. | ||
| + | * Если дискриминант равен нулю, оба действительных корня совпадают и для простоты говорят, что уравнение имеет один корень. | ||
| + | * Если дискриминант отрицательный, школьникам обычно говорят, что уравнение корней не имеет. | ||
| + | |||
| + | На самом деле, уравнение не имеет лишь действительных корней. Как становится известно при дальнейшем изучении математики, в этом случае имеются два комплексносопряженных корня, но пока будем считать, что при D < 0 уравнение корней не имеет. Лица, продвинутые в математике, могут при вычислении дискриминанта явно указать тип complex и не тратить время на всякие анализы. Остальным следует использовать тип real. | ||
| + | |||
| + | Корни квадратного уравнения определяются по формуле | ||
| + | |||
| + | [[Файл:Ser.png|300px]] | ||
| + | |||
| + | Из приведенной формулы понятно, почему при D = 0 получаются два равных по значению корня. Также понятно, почему при D < 0 говорят, что корней нет: возникает проблема с извлечением квадратного корня из отрицательного числа. | ||
| + | |||
| + | Найти корни квадратного уравнения ax<sup>2</sup>+bx+c=0, если a≠0. Коэффициенты a, b и c ввести с клавиатуры. Вывод осуществить с точностью 5 знаков после запятой. Если действительных корней нет, вывести соответствующее сообщение. | ||
| + | |||
| + | <syntaxhighlight lang="pascal" line> | ||
| + | ## | ||
| + | ## | ||
| + | var (a, b, c) := ReadReal3('Введите коэффициенты a, b, c:'); | ||
| + | var D := b * b - 4 * a * c; | ||
| + | if D > 0 then // два разных корня | ||
| + | begin | ||
| + | D := Sqrt(D); | ||
| + | var x1 := (-b - D) / (2 * a); | ||
| + | var x2 := (-b + D) / (2 * a); | ||
| + | Write('x1 = ', x1:0:5, ', x2 = ', x2:0:5) | ||
| + | end | ||
| + | else if D = 0 then | ||
| + | Write('x = ', -b / (2 * a):0:5) | ||
| + | else | ||
| + | Print('Корней нет'); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Введите коэффициенты a, b, c: 3.8 -10 4 | ||
| + | x1 = 0.49197, x2 = 2.13960 | ||
| + | |||
| + | == Существует ли треугольник? == | ||
| + | Даны три отрезка прямой длиной a, b и c. Можно ли из них составить треугольник? | ||
| + | Из геометрии известно условие существования треугольника: сумма длин двух любых его сторон должна быть больше длины третьей. Этим условием и нужно воспользоваться. | ||
| + | |||
| + | <syntaxhighlight lang="pascal" line> | ||
| + | ## | ||
| + | var (a, b, c) := ReadReal3('Введите длины сторон треугольника:'); | ||
| + | if (a + b > c) and (a + c > b) and (b + c > a) then | ||
| + | Print('Треугольник можно построить') | ||
| + | else | ||
| + | Print('Треугольник построить нельзя'); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Прямоугольный ли треугольник? == | ||
| + | Даны три отрезка прямой длиной a, b и c. Можно ли из них составить прямоугольный треугольник? | ||
| + | К условию существования треугольника из предыдущей задачи нужно добавить еще одно условие: в треугольнике должна выполняться теорема Пифагора. Квадрат большей из сторон (это будет гипотенуза) должен равняться сумме квадратов катетов (двух меньших сторон). Можно обеспечить нахождение в переменной с наибольшего из введенных значений. А можно каждой тройки значений набора {a, b, c} проверить выполнение теоремы Пифагора. Последний вариант записывается короче. | ||
| + | |||
| + | <syntaxhighlight lang="pascal" line> | ||
| + | ## | ||
| + | var (a, b, c) := ReadReal3('Введите длины сторон треугольника:'); | ||
| + | if (a + b > c) and (a + c > b) and (b + c > a) then | ||
| + | if (a * a + b * b = c * c) or (a * a + c * c = b * b) or (b * b + c * c = a * a) then | ||
| + | Print('Можно построить прямоугольный треугольник') | ||
| + | else | ||
| + | Print('Можно построить непрямоугольный треугольник') | ||
| + | else | ||
| + | Print('Треугольник построить нельзя'); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Введите длины сторон треугольника: 15 20 25 | ||
| + | Можно построить прямоугольный треугольник | ||
Текущая версия на 20:06, 9 мая 2023
Поиск минимумов и максимумов
Найти минимальное из двух произвольных чисел.
Если сказано, что числа произвольные, выбираем для них тип real. Алгоритм поиска минимума среди чисел a и b следующий: если а < b, минимум равен a, иначе он равен b.
1 ##
2 var (a, b) := ReadReal2('Введите два числа:');
3
4 if a < b then
5 Print('Минимум равен', a)
6 else
7 Print('Минимум равен', b);
8
9 Println('Минимум равен', if a < b then a else b);
10
11 Println('Минимум равен', (a < b) ? a : b);
Найти максимальное из трех целых чисел.
Сначала найдем максимальное из первой пары чисел, а затем сравним результат с третьим числом.
1 ##
2 var (a, b, c) := ReadInteger3('Введите три целых числа;');
3 var m := if a > b then a else b;
4 m := if m > c then m else c;
5 Print('Максимум:', m);
Введите три целых числа; 4 7 2 Максимум: 7
Короткое альтернативное решение:
1 ##
2 var (a, b, c) := ReadInteger3('Введите три целых числа;');
3 Print('Максимум:', Max(a, b, c));
Процент отклонения значения максимального из чисел от среднего значения
Даны четыре натуральных числа. Найти процент отклонения значения максимального из чисел от среднего значения всех чисел с точностью до двух знаков после запятой.
1 ##
2 var a, b, c, d: integer;
3 Write('Введите четыре целых числа: ');
4 Read(a, b, c, d);
5 var mx := Max(a, b, c, d);
6 var m := (a + b + c + d) / 4;
7 Write('Отклонение составляет ', (mx - m) / m * 100:0:2, '%');
Введите четыре целых числа: 29 31 32 31 Отклонение составляет 4.07%
Анализ цифр в числе заданной разрядности
Если заданное трехзначное число читается одинаково слева направо и справа налево, вывести «Да». В противном случае вывести «Нет».
Число трехзначное, поэтому для выполнения приведенного в задании условия достаточно, чтобы первая цифра числа равнялась последней.
1 ##
2 var n := Abs(ReadInteger('Введите трехзначное число:'));
3 Print(if n div 100 = n mod 10 then 'Да' else 'Нет');
Введите трехзначное число: 161 Да
Решение линейных и квадратных уравнений
Линейное уравнение
Линейное уравнение имеет вид ax + b = 0, где a ≠ 0. Его решением (корнем) является значение x = -b / a. В некоторых задачах, особенно олимпиадных, намеренно содержащих препятствия к получению корректного решения, значение a = 0 также считается допустимым, несмотря на то, что математически оно приводит к вырожденности линейного уравнения – об этом следует помнить.
Вычисление х производится при помощи операции деления «/», перед делением операнды приводятся к вещественному типу, так что лучше сразу определить для переменных a и b тип real.
Написать программу для решения уравнения ax + b = 0. Значения a и b ввести с клавиатуры. Рассмотреть случаи, когда уравнение может иметь множество корней или не иметь корней вообще.
Корень линейного уравнения определяется по формуле x = -b / a. При a = 0 возможны два случая. Если b = 0, исходное уравнение обращается в тождество 0 ≡ 0 при любом х и корней бесчисленное множество. При b ≠ 0 исходное уравнение принимает вид b = 0, что противоречит рассматриваемому значению, поэтому уравнение в этом случае корней не имеет. Для коэффициентов а и b выбираем тип real. Следует помнить, что если взять значение а достаточно близким к нулю, появится шанс получить «машинную бесконечность».
1 ##
2 var (a, b) := ReadReal2('Введите коэффициенты a и b:');
3 if a = 0 then
4 if b = 0 then
5 Print('Корней бесконечное множество')
6 else
7 Print('Корней нет')
8 else
9 Print('x =', -b / a);
Введите коэффициенты a и b: 0.18 3.173 x = -17.6277777777778
Квадратное уравнение
Квадратное уравнение в общем виде записывается как ax2 + bx + c = 0, где a ≠ 0. Такие уравнение обычно решают при помощи вычисления вспомогательной величины – дискриминанта. Дискриминант определяется формулой D = b2 – 4ac.
- Если дискриминант положительный, уравнение имеет два разных действительных корня.
- Если дискриминант равен нулю, оба действительных корня совпадают и для простоты говорят, что уравнение имеет один корень.
- Если дискриминант отрицательный, школьникам обычно говорят, что уравнение корней не имеет.
На самом деле, уравнение не имеет лишь действительных корней. Как становится известно при дальнейшем изучении математики, в этом случае имеются два комплексносопряженных корня, но пока будем считать, что при D < 0 уравнение корней не имеет. Лица, продвинутые в математике, могут при вычислении дискриминанта явно указать тип complex и не тратить время на всякие анализы. Остальным следует использовать тип real.
Корни квадратного уравнения определяются по формуле
Из приведенной формулы понятно, почему при D = 0 получаются два равных по значению корня. Также понятно, почему при D < 0 говорят, что корней нет: возникает проблема с извлечением квадратного корня из отрицательного числа.
Найти корни квадратного уравнения ax2+bx+c=0, если a≠0. Коэффициенты a, b и c ввести с клавиатуры. Вывод осуществить с точностью 5 знаков после запятой. Если действительных корней нет, вывести соответствующее сообщение.
1 ##
2 ##
3 var (a, b, c) := ReadReal3('Введите коэффициенты a, b, c:');
4 var D := b * b - 4 * a * c;
5 if D > 0 then // два разных корня
6 begin
7 D := Sqrt(D);
8 var x1 := (-b - D) / (2 * a);
9 var x2 := (-b + D) / (2 * a);
10 Write('x1 = ', x1:0:5, ', x2 = ', x2:0:5)
11 end
12 else if D = 0 then
13 Write('x = ', -b / (2 * a):0:5)
14 else
15 Print('Корней нет');
Введите коэффициенты a, b, c: 3.8 -10 4 x1 = 0.49197, x2 = 2.13960
Существует ли треугольник?
Даны три отрезка прямой длиной a, b и c. Можно ли из них составить треугольник?
Из геометрии известно условие существования треугольника: сумма длин двух любых его сторон должна быть больше длины третьей. Этим условием и нужно воспользоваться.
1 ##
2 var (a, b, c) := ReadReal3('Введите длины сторон треугольника:');
3 if (a + b > c) and (a + c > b) and (b + c > a) then
4 Print('Треугольник можно построить')
5 else
6 Print('Треугольник построить нельзя');
Прямоугольный ли треугольник?
Даны три отрезка прямой длиной a, b и c. Можно ли из них составить прямоугольный треугольник?
К условию существования треугольника из предыдущей задачи нужно добавить еще одно условие: в треугольнике должна выполняться теорема Пифагора. Квадрат большей из сторон (это будет гипотенуза) должен равняться сумме квадратов катетов (двух меньших сторон). Можно обеспечить нахождение в переменной с наибольшего из введенных значений. А можно каждой тройки значений набора {a, b, c} проверить выполнение теоремы Пифагора. Последний вариант записывается короче.
1 ##
2 var (a, b, c) := ReadReal3('Введите длины сторон треугольника:');
3 if (a + b > c) and (a + c > b) and (b + c > a) then
4 if (a * a + b * b = c * c) or (a * a + c * c = b * b) or (b * b + c * c = a * a) then
5 Print('Можно построить прямоугольный треугольник')
6 else
7 Print('Можно построить непрямоугольный треугольник')
8 else
9 Print('Треугольник построить нельзя');
Введите длины сторон треугольника: 15 20 25 Можно построить прямоугольный треугольник